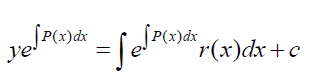SPEEDCUBING: Maret 2020

Assalamu Alaikum Warahmatullahi Wabarakatuh
Selamat pagi bagi yang membacanya di pagi hari
Selamat siang bagi yang membacanya di siang hari
Selamat sore bagi yang membacanya di sore hari
Selamat malam bagi yang membacanya di malam hari
Kali ini kita akan membahas PERSAMAAN DIFFERENSIAL BIASA

Persamaan Differensial merupakan suatu persamaan yang meliputi turunan fungsi dari satu atau lebih variabel terikat terhadap satu atau lebih variabel bebas disebut Persamaan Difrensial. Selanjutnya jika turunan fungsi itu hanya tergan tung pada satu variabel bebas maka disebut Persamaan Difrensial Biasa.

contoh persamaan differensial biasa

Orde dan Derajat Persamaan Diferensial

1. Penentuan pangkat dan derajat suatu persamaan diferensial tergantung pada kandungan fungsi turunan di dalam persamaan diferensial tersebut.

2. Orde atau pangkat suatu persamaan diferensial merupakan pangkat tertinggi dari turunan yang muncul dalam persamaan diferensial.

3. Degree atau derajat dari suatu persamaan diferensial adalah pangkat dari suku yang memuat turunan tertinggi dalam persamaan diferensial (pangkat dari orde).

(1) PDB Orde Dua Derajat Satu

(2) PDB Orde Dua Derajat Tiga

(3) PDB Orde Satu Derajat Dua

Persamaan Diferensial Linear dan Tak Linear
Suatu persamaan diferensial dikatakan liniar jika tidak ada perkalian antar variabel-variabel tak bebas dan derivatif-derifatifnya atau dapat ditulis dalam bentuk:

Persamaan ini merupakan kasus khusus dari bentuk umum PD yang disebut dengan Persamaan Diferensial Linear orde n.

Persamaan diferensial yang tidak dapat ditulis dalam bentuk ini disebut persamaan diferensial tak linear.

Selain itu, persamaan diferensial yang tak linear dalam beberapa variabel tak bebas dikatakan tak liniar dalam variabel tersebut.

Persamaan diferensial yang tak liniar dalam himpunan semua variabel tak bebas secara sederhana dikatakan tak linear.

jawab:

Linear dalam y

Tak linear dalam y karena memuat yy'

Linear dalam setiap variabel tak bebas x atau y, namun tak linear dalam himpunan {x,y}, sehingga PD tak linear

Tak linear

Tak linear

Menemukan Persamaan Diferensial

Menemukan persamaan diferensial dapat dilakukan dengan langkah-langkah sebagai berikut: Hitunglah banyaknya konstanta sembarang yang terdapat dalam persamaan yang akan dicari bentuk persamaan diferensialnya.

Hilangkan semua konstanta sembarang itu dengan cara eliminasi.

Jika konstanta sembarang sebanyak n, maka dibutuhkan n + 1 persamaan untuk melakukan eliminasi. n + 1 persamaan dapat diperoleh dengan cara mendiferensialkan persamaan semula sampai turunan ke-n.

Banyaknya konstanta sembarang menunjukkan pangkat tertinggi dari turunan dalam persamaan diferensial yang dicari.

jawab:

1. Karena terdapat 1 konstanta, maka dibutuhkan 2 persamaan untuk memperoleh bentuk persamaan diferensial yang dicari. Persamaan kedua dapat diperoleh dengan melakukan diferensiasi pada persamaan awal.

2. Dengan cara yang sama, persamaan ini dapat kita selesaikan sebagai berikut:

3. Dari turunan pertama dan kedua diperoleh

CONTOH SOAL

1. Diketahui f’(x) ialah turunan dari f(x) = 5x³+ 2x²+ 6x + 10, Tentukan nilai f’(x) ialah

2. Sebuah turunan pertama dari f(x) = sin³(3x² – 3) ialah f‘(x) =
3. Identifikasi orde dari persamaan differensial

JAWAB:

1. f(x) = 5x³ +2x² + 6x + 10
     f’(x) = 15x²+ 4x +5
    f’(3) = 15 . 3²+4 . 3 + 5
            = 135 + 12 + 5
            = 152
2. f(x) = sin³(3x² – 3)

    f’(x) = sin^(3-1)(3x² – 3).3.6x.cos (3x² – 3)
            = 18x sin²(3x² – 3) cos (3x² – 3)
3. orde satu
4.

PDB ORDE 1

1. Dengan Variabel Terpisah
Persamaan diferensial berbentuk y’ = f(x), dengan f suatu fungsi kontinu pada suatu interval real, dapat dicari penyelesaiannya dengan cara mengintegralkan ke dua ruas. Akan tetapi perhatikan bila persamaan diferensial berbentuk dy/dx=f(x,y)
yang turunannya adalah suatu fungsi dalam dua variabel x dan y. Untuk mencari penyelesaian diatas kadang tidak mudah. Bila f(x,y) dapat difaktorkan ke faktor-faktor yang hanya memuat x atau y, yakni dy/dx=f(x,y)= p(x) q(y) atau d(y)/q(y) = p(x) dx
maka persamaan diferensial ini merupakan persamaan diferensial dengan variabel terpisah.Solusi persamaan diferensial dapat dicari dengan cara mengintegralkan kedua ruas (terhadap variabel yang sama yakni x). Pengintegralan seperti ini dapat dilakukan sebab diasumsikan y sebagai fungsi dari x. Ruas kiri persamaan diferensial

sehingga diperoleh

Selanjutnya bila dimisalkan u = y(x) dan du = y’(x) dx,maka dengan mengintegralkan kedua ruas persamaan menghasilkan solusi

contoh

carilah penyelesaian umum PD (4x+6xy²)dx+3(y+x²y)dy=0

2. Fungsi Homogen

Suatu persamaan diferensial f (x, y ) dx + g (x, y ) dy = 0 dikatakan homogen jika f (x, y ) dan g (x,y) adalah homogen berderajat sama, atau dapat dinyatakan dalam bentuk

Sementara itu, sifat homogenitas fungsi f dan g dapat diketahui melalui de…finisi berikut.

Suatu fungsi f (x, y ) dikatakan homogen berderajat nol jika f (λx, λy ) = f (x, y )

untuk semua nilai positif dari λ dengan (λx, λy ) dalam domain dari f .Secara umum, f (x, y ) dikatakan homogen berderajat n jika terdapat λ sedemikian sehingga f (λx, λy ) = λ^n f (x, y )

contoh

fungsi

adalah homogen berderajat nol sebab

contoh

Tunjukkan bahwa fungsi berikut, homogen berderajat 3

solusi

3. PDB Linear

PDB Linear adalah PDB yang dapat dituliskan dalam bentuk : y'+p(x)y=r(x)

Penyelesaian :

kalikan kedua ruas dengan faktor integral

Integralkan kedua ruas terhadap x

Solusi Umum PDB linear :

contoh

Selesaikan persamaan diferensial xy'-2y=x^3 e^x

PDB ORDE 2

Bentuk umum : y''+ p(x)y'+ g(x)y= r(x)

p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan Differensial diatas disebut homogen, sebaliknya disebut non homogen.

Persamaan Differensial Biasa linier orde dua homogen dengan koefisien konstan, memiliki bentuk umum : y''+ ay'+ by= 0 dimana a, b merupakan konstanta sebarang.

1.Homogen

Diketahui y''+ ay'+ by= 0 Bentuk umum solusi: y = c1y1+ c2y2

Misalkany =e^rx

Persamaannya berubah menjadi r^2+ ar+ b = 0, sebuah persamaan kuadrat

Jadi kemungkinan akarnya ada 3 yaitu:

1. Akar real berbeda (r1,r2; dimana r1≠r2)

Memiliki solusi basis y1= e^r1xdan y2= e^r2x dan mempunyai solusi umum

2. Akar real kembar (r1,r2; dimana r = r1=r2) Memiliki solusi basis y1= e^rx dan y2=xe^rx dan mempunyai solusi umum

3. Akar kompleks kojugate (r1= u + wi, r2= u –wi)

Memiliki solusi basis y1= e^ux cos wx; dan y2= e^ux sin wx dan mempunyai solusi umum

contoh soal:

y''+5y'+6y+0

persamaan karakteristiknya ( r + 2 ) ( r + 3 ) = 0

r1 = -2 atau r2 = -3

maka solusinya : C1e^-2x +C2e^-3x

2. Non Homogen

Bentuk umum:y''+ p(x)y'+ g(x)y= r(x) dengan r(x)≠0

Solusi total :y= yh+ yp
Dimana yh= solusi PD homogen
yp= solusi PD non homogen
Menentukan yp

a. Metode koefisien tak tentu

b. Metode variasi parameter

a.metode koefisien tak tentu

pilihlah yp yang serupa dengan r(x), lalu substitusikan ke dalam persamaan.

Solusi partikular tidak boleh muncul pada solusi homogennya. Jika hal ini terjadi, kalikan solusi khususnya dengan faktor x atau x^2 sehingga tidak memuat lagi solusi homogennya.

contoh

y''-3y'-2y=e^-x

penyelesaian