SPEEDCUBING: TURUNAN DAN INTEGRAL

TURUNAN DAN INTEGRAL

Assalamu Alaikum Warahmatullahi Wabarakatuh
Selamat pagi bagi yang membacanya di pagi hari
Selamat siang bagi yang membacanya di siang hari
Selamat sore bagi yang membacanya di sore hari
Selamat malam bagi yang membacanya di malam hari
Kali ini kita akan membahas Turunan dan Integral

TURUNAN

Menurut Herakleitos seorang filsuf Yunani kuno dia mengatakan “hal yang paling mendasar, yang paling esensial yaitu adanya perubahan”.

Misalnya seseorang lima tahun yang lalu dengan tahun sekarang itu pasti mengalami perubahan. Namun dalam sains perubahan sekaligus ada pola-pola yang konstan yaitu hukum alam yang telah Tuhan tetapkan di alam semesta yang bisa kita pelajari.

Misalkan ada grafik seperti di bawah ini

Jika kita mencari gradien diatas, maka kita perlu membuat garis lurus dari titik (x,f(x)) ke titik (x+Δ x) dan akan menjadi

Untuk mencari kemiringan, kita menggunakan rumus depan/samping

Karena rumus diatas cuma berlaku pada garis lurus antara titik (x,f(x)) dengan (x+∆x), maka kita akan memperdekat jaraknya seperti di bawah ini

Maka ini akan terlihat lurus. Lalu bagaimana jika kita membuat banyak titik di grafik tersebut sehingga akan memiliki banyak gradien atau kemiringan seperti dibawah ini

Maka diferensial itu sebenarnya mencari kelajuan daripada perubahan dari Y terhadap X

contoh:

Dan jika kita menurunkan setiap sifat umum suatu soal, maka kita akan dapat turunan umum seperti:

Untuk fungsi trigonometri

Misalkan y= sin x

Dan jika kita menurunkan setiap sifat umum suatu soal trigonometri, maka kita akan dapat turunan umum seperti:

Turunan fungsi (operasi aljabar fungsi)

Contoh:

untuk memudahkan kita mengingat turunan dari perkalian 2 fungsi TURUNAN FUNGSI PERTAMA DIKALI FUNGSI KEDUA (TIDAK DILAKUKAN PENURUNAN) + FUNGSI PERTAMA (TIDAK DILAKUKAN PENURUNAN) DIKALI TURUNAN FUNGSI KEDUA

contoh:

INTEGRAL

Secara mudah integral dapat diartikan sebagai kebalikan dari differensial atau turunan. Lambang integral adalah ∫. Integral dari suatu fungsi misalnya F(x)= ∫f(x)dx memiliki tujuan untuk menghitung luas daerah dibawah kurva. Jadi jika ada suatu daerah yang memiliki bentuk yang rumit yang tidak memiliki rumus untuk mencari luas daerah seperti yang dipelajari dalam geometri, kita bisa mencari luas daerah tersebut menggunakan integral.

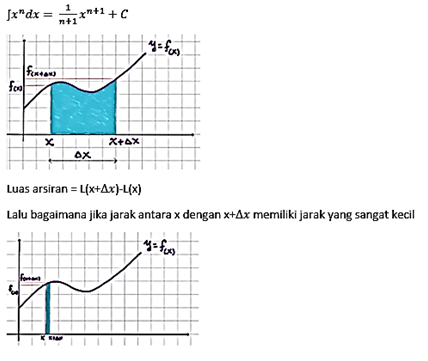
Di pembahasan sebelumnya yaitu turunan, kita sudah tau bahwa jika