Selamat pagi bagi yang membacanya di pagi hari
Selamat siang bagi yang membacanya di siang hari
Selamat sore bagi yang membacanya di sore hari
Selamat malam bagi yang membacanya di malam hari
Kali ini kita akan membahas PERSAMAAN DIFERENSIAL BERNOULLI
1. Bentuk Umum
Jika m>0, akan diperoleh persamaan-persamaan yang jelas lebih mudah untuk
diselesaikan.
2. Metode Penyelesaian
a. PD bersangkutan harus dapat disusun ulang dalam bentuk LINIER, yaitu dengan
membagi kedua ruas dengan faktor y pangkat m, sehingga
b. Lakukan substitusi fungsi yang dicari, yang didefinisikan sebagai:
c. Karena y merupakan fungsi dari x , maka turunan dari fungsi z adalah:
d. Sehingga, solusi dari PD yang dimaksudkan dapat ditulis sebagai:
3. Contoh Soal
sekian materi untuk kali ini
Wassalamu Alaikum Warahmatullahi Wabarakatuh


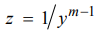
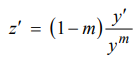










 .......(Persamaan 1)
.......(Persamaan 1)











