Selamat siang bagi yang membacanya di siang hari
Selamat sore bagi yang membacanya di sore hari
Selamat malam bagi yang membacanya di malam hari
Tingkat Persamaan Diferensial dapat dilihat dari turunan tertinggi yang termuat dalam Persamaan Diferensial itu.
Bentuk umum PD Linier orde-n adalah
a0(x)y(n)+a1(x)y(n-1)+…+an-1(x)y’+an(x)y = F(x)
PD yang tidak dapat dinyatakan dalam bentuk di atas dikatakan tidak linier.
Contoh:
Jika F(x) pada persamaan PD Linier orde-n sama dengan nol maka PD disebut PD homogen atau tereduksi atau komplementer. Jika F(x)≠0 maka PD disebut PD lengkap atau PD tak homogen.
Contoh:
Jika a0(x), a1(x), ...., an(x) adalah konstanta maka PD disebut PD Linier dengan koefisien konstanta, jika tidak disebut PD Linier koefisien variabel. Bentuk dy/dx ,d^2y/dx^2 , d^n y/dx^n dapat dituliskan dengan lambang Dy, D2y, …, Dny, dengan D,D2… disebut operator diferensial. Sehingga persamaan PD Linier orde-n dapat dinyatakan sebagai:
1. Teorema dasar persamaan diferensial linier
Untuk menyelesaikan PD Linier berbentuk
(D)y = F(x) dengan F(x) ≠0,
kita misalkan Yc(x) adalah solusi umum PD homogen dari (D)y=0, maka penyelesaian umum PD Linier adalah dengan menjumlahkan penyelesaian umum PD homogen dan penyelesaian khusus, yaitu:
y = Yc(x) + Yp(x)
contoh:
Solusi umum PD homogen: (D2-3D+2)y=0 adalah y=c1ex+c2e2x dan
solusi khusus PD : (D2-3D+2)y=4x2 adalah 2x2+6x+7,
maka solusi umum PD lengkap/tak homogen dari
(D2-3D+2)y=4x2 adalah y= c1ex+c2e2x+2x2+6x+7
2. Ketakbebasan linier
Himpunan n fungsi y1(x), y2(x), …, yn(x) dikatakan takbebas linier pada suatu selang jika ada n konstanta c1, c2, …, cn yang tidak semua nol, sehingga berlaku:
c1 y1(x)+ c2 y2(x)+ …+ cn yn(x) = 0
jika tidak maka himpunan fungsi tersebut dikatakan bebas linier.
Contoh:
2e3x, 5e3x,e-4x
Tak bebas linier pada suatu selang karena dapat ditentukan konstanta c1, c2, c3 yang tidak semua nol sehingga:
c1(2e3x)+ c2 (5e3x)+c3 (e-4x) = 0 dengan c1 =-5, c2 =2, c3 =0
Contoh:
ex dan xex adalah bebas linier karena c1(ex)+ c2 (xex)=0 hanya jika c1 =0,
c2 =0
3. determinan wronski
Himpunan fungsi y1(x), y2(x), …, yn(x) (yang mempunyai turunan) adalah bebas linier pada suatu selang jika determinan:
Determinan tersebut dinamakan determinan Wronski.
Contoh:
Tentukan determinan Wronski (Wronskian) untuk fungsi-fungsi berikut:
a. (sin 3x,cos 3x)
Contoh
Tunjukkan himpunan fungsi adalah takbebas linier untuk semua nilai x!
a. kita dapat menunjukkan dengan memilih konstanta c1, c2, c3 yang tidak semuanya nol sehingga c1(1-x)+c2(1+x)+c3(1-3x)=0, jika ditentukan c1=1, c2=-1, c3=0 maka 1-x-1-x+0=0, sehingga himpunan fungsi adalah takbebas linier.
b. kita juga dapat menghitung determinan Wronski-nya, yaitu:
terbukti bahwa Wronskian = 0 berarti himpunan fungsi tak bebas linier untuk semua x
4. Prinsip superposisi
Jika y1(x), y2(x), …, yn(x) adalah n penyelesaian bebas linier dari persamaan linier orde-n, (D)y=0 maka solusi umumnya:
y = c1y1(x) + c2y2(x) + …+ cnyn(x)
Contoh:
Jika y1(x) dan y2(x) adalah solusi persamaan diferensial homogen y’’+P(x)y’+Q(x)y=0 maka kombinsi linier c1y1(x)+c2y2(x) juga solusi persamaan diferensial.
Bukti:
y1(x) dan y2(x) solusi y’’+Py’+Qy’= 0 maka
y1’’+ Py1’+ Qy1 = 0 dan
y2’’+ Py2’+ Qy2 = 0
dari solusi y = c1y1 + c2y2, maka
y’=c1y1’+ c2y2’
y’’=c1y1’’+ c2y2’’
subtitusi ke persamaan diferensial diperoleh:
y’’+ P(x)y’+ Q(x)y = 0
c1y1’’+ c2y2’’+ P(c1y1’+c2y2’) + Q(c1y1+c2y2) = 0
c1y1’’+ c2y2’’+ c1Py1’+ c2Py2’+ c1Qy1+ c2Py2 = 0
c1(y1’’+ Py1’+ Qy1) + c2(y2’’+ Py2’+ Qy2) = 0
c1.0 + c2.0 = 0
SEKIAN MATERI KALI INI



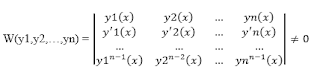


Tidak ada komentar:
Posting Komentar