Selamat pagi bagi yang membacanya di pagi hari
Selamat siang bagi yang membacanya di siang hari
Selamat sore bagi yang membacanya di sore hari
Selamat malam bagi yang membacanya di malam hari
Kali ini kita akan membahas PERSAMAAN DIFFERENSIAL TERPISAH
Suatu persamaan diferensial variabel
terpisah ditandai oleh fakta bahwa dua peubah dari persamaan itu bersama-sama
masing-masing dideferensiannya, dapat ditempatkan di ruas yang berlawanan.
Dengan manipulasi aljabar, memungkinkan kita menuliskan persamaan diferensial
terpisah dalam bentuk implisit:
dy/dx = P(x)/Q(x) >>>(dalam bentuk eksplisit)
Untuk memperoleh penyelesaian umum
suatu persamaan diferensial terpisah, pertama-tama kita pisahkan kedua peubah
dan kemudian integralkan kedua ruas.
awal →
Q(y) dy = P(x) dx
integral → ∫ P(x) dx = ∫ Q(y) dy + C, dimana C adalah konstanta
sembarang
Note:
Bisa dilakukan hanya pada variabel yang sama,
Hanya mengandung variabel y ← (y + 1 / y2 + 4) dy = -x dx → Hanya
mengandung variabel x
contoh soal
1.Carilah solusi umum dari persamaan diferensial berikut:
x² dx + (1-y²) dy = 0
Karena PD berbentuk variabel terpisah, maka penyelesaian dapat ditemukan dengan melakukan pengintegralan langsung pada tiap-tiap ruas
Dengan demikian, solusi umum PD adalah
Perhatikan bahwa PD dapat ditulis kembali dalam bentuk
Dengan melakukan pengintegralan dikedua ruas, diperoleh
Ubah bentuk PD ke bentuk variabel terpisah, kemudian selesaikan dengan pengintegralan
Dengan demikian solusi umum PD adalah
4. y2 dy = (x + 3x2) dx, bila mana x = 0 dan y = 6 → bentuk Implisit
y2 dy = (x + 3x2) dx, syarat harus mengandung variabel yang sama pada tiap ruas.
Integralkan kedua ruas
Menghitung
konstanta C, kita menggunakan persyaratannya bilamana x = 0 dan y = 6, maka
akan menghasilkan C = 216
Solusi khususnya
adalah :
ubah ke dalam eksplisit
xy (dy/dx) + x2 + 1 = 0
Bagi
tiap-tiap ruas
y dy = -(x2 + 1/x) dx
integralkan kedua ruas
Maka, solusi umumnya adalah y2 = -x2/2 – ln|x + c
untuk soal dan pembahasan lebih lanjut, buka link di bawah ini:
https://dekuwissengngi.blogspot.com/2020/04/soal-persamaan-diferensial-terpisah.html

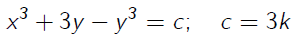



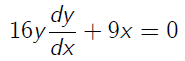





Tidak ada komentar:
Posting Komentar